"Cellular processes generally involve interactions among 101 to 105 gene products. These interactions can be both biochemical, as in the activation of one protein by another, and mechanical, as in the application of force between bodies. Even when each individual interaction is simple and understood in detail neither intuition nor qualitative description can forecast the emergent behavior of the whole system." This introduction from Alberts and Odell (2004) is the central tenet of our efforts at modeling cellular processes: we believe that fully understanding these inherently complex systems requires mathematical modeling/simulation of the small-scale details. We are continually refining our computer model of the motility of the bacteria Listeria monocytogenes in an effort to better understand one such complex system. L. monocytogenes motility is well studied experimentally. Our model simulates both the biochemical kinetics (often measured by experiment) and the mechanical dynamics (which obey the laws of classical mechanics) of this system in hopes of capturing and understanding the complex system behaviors.
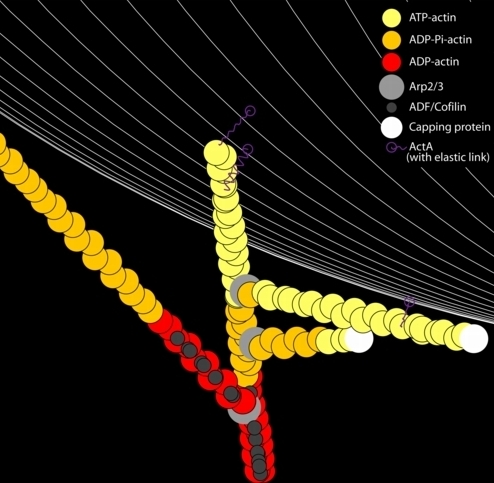
As a way of introduction to the model, consider this legend figure (a cleaned-up movie frame) showing a single branching structure in close proximity to the bacterial surface (white lines). There is a single mother filament from which daughter filaments branch at ~70 degrees, mediated by an activated Arp2/3 complex which is incorporated into the structure at the branch point. Each filament is comprised of actin monomers in one of three flavors determined by the state of the associated nucleotide: ATP actin (young f-actin), ADP-Pi actin (hydrolyzed but the inorganic phosphate has not yet dissociated), and ADP actin (old f-actin). The old (ADP) actin has a high affinity for ADF/Cofilin, which enhances the deconstruction of the actin network. F-actin locations that are interacting with the bacterial surface-bound ActA proteins can form a new branch (with an Arp2/3 concentration dependent probability) and f-actin barbed-ends that are near such an interaction are protected from capping.
|
|
A movie frame/legend demonstrates many features of our in silico reconstitution: polymerization, hydrolysis of the actin-bound nucleotide, capping, Arp2/3 mediated branching, ADF/Cofilin binding, and ActA interactions. |
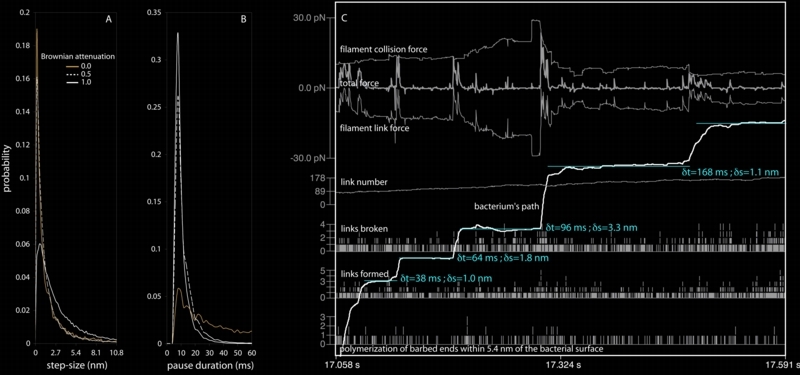
In 2000, Scot Kuo and James McGrath reported their observations of nanoscale stepping in the motion of L. monocytogenes in vivo (Kuo and McGrath 2000). Using an adapted laser-tweezers device at low power they characterized this small-scale stepping, finding that the steps were often 5.4 nm in magnitude (the diameter of an actin monomer). When we examined our simulated bacterial trajectories at this length scale we were surprised to see nanometer scale stepping and curious to find our characteristic step-size. Would it match the experimental result? After much hair pulling, incomprehension, and analysis we came to realize that our "steps" have no characteristic size; they are distributed as with a Poisson process, with smaller step-sizes occurring more frequently than larger ones. Additionally, an analysis of pause duration, i.e. the time-interval between adjacent steps, implies a random process at work in delimiting pause entry and exit.
|
|
A and B are histograms of step-size and pause duration assembled from many thousand of pause-step events. The Brownian attenuation factor refers to the amplitude of simulated Brownian motion for the bacterium (see Alberts & Odell 2004 for details). C is a look at how several system values change during several adjacent pause-step events for the case in which there is no Brownian motion of the bug at all. This case provides the clearest look at the interplay between collision and link forces; a step occurs when the filament link force, which had previously balanced the collision forces, plummets as a result of cascading breakage of links. More analysis and discussion of this behavior can be found in Alberts and Odell (2004). |
There are several differing experimental measurements and theoretical/computational predictions regarding Listeria's force-velocity curve. Many independent observations support the ability of this bug to power through cellular obstacles (e.g. mitochondria) and laser tweezers have failed to stall the bacterium's motion (Gerbal et al 2000). Adding methylcellulose to the media increases the apparent viscosity for larger objects (i.e. L. monocytogenes) without disturbing actin polymerization kinetics. Two groups have used this technique to generate experimental force-velocity curves in vitro and have come to seemingly contradictory conclusions. McGrath et al (2003) find that velocity falls off exponentially with increasing viscosity (force). Wiesner et al (2003), using beads instead of bugs, find a relatively flat velocity curve with increasing viscosity (force). In the theoretical camp, Gerbal et al (2000) and Mogilner and Oster (2003) have presented analysis supportive of the exponential dependence of velocity on resisting force, while the work of Carlsson (2001) supports a flat force-velocity relationship. Carlsson (2001), Mogilner and Oster (2003), and McGrath et al (2003) have all predicted/measured an increased filament density in the tail at higher loads. We are presently examining the effects of higher viscous loads on our virtual bacterium... preliminary data falls nicely along the curves measured by McGrath et al (2003), but with some additional surprising results.
|
|
A movie showing the effect of increasing the viscous drag on the bacteria in our simulations. This computational experiment is designed to mimic the addition of methylcellulose as in McGrath et al (2003) and Wiesner et al (2003). |
The bacterial surface protein ActA, expressed by Listeria, is sufficient to bypass normal cell regulation of actin growth and impart motility to that bug. Small man-made beads of different types have been coated with purified ActA and will then jet around inside of cells, cytoplasmic extracts, or motility mediums created from purified proteins. The symmetry of spherical beads, and induced asymmetries, make this motility system ideal for studying the dependence of motility on geometry and ActA distribution. Stay tuned for more on bead simulations.
|
|
An early (in development) bead simulation... check back for biologically motivated bead simulations |